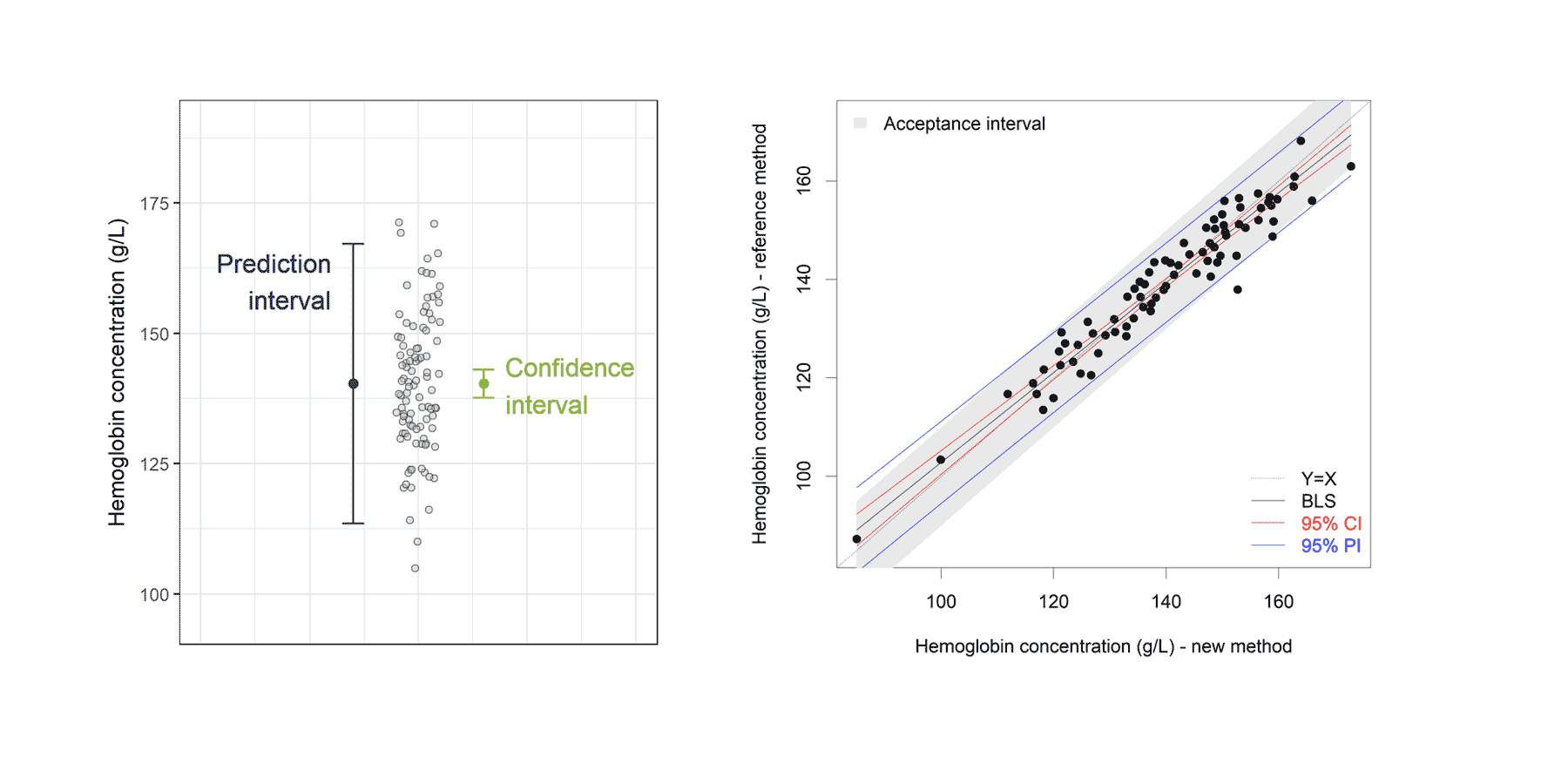
In this post, I will illustrate the use of prediction intervals for the
comparison of measurement methods. In the example a new spectral method
for measuring whole blood hemoglobin is compared with a reference
method.
But first, let’s start with discussing the large difference between a
confidence interval and a prediction interval.
Prediction interval versus Confidence interval
Very often a confidence interval is misinterpreted as a prediction
interval, leading to unrealistic “precise” predictions. As you will see,
prediction intervals (PI) resemble confidence intervals (CI), but the
width of the PI is by definition larger than the width of the CI.
Let’s assume that we measure the whole blood hemoglobin concentration in
a random sample of 100 persons. We obtain the estimated mean (Est_mean),
limits of the confidence interval (CI_Lower and CI_Upper) and limits of
the prediction interval (PI_Lower and PI_Upper):
(The R-code to do this is in the next paragraph)
| Est_mean | CI_Lower | CI_Upper | PI_Lower | PI_Upper |
|---|---|---|---|---|
| 140 | 138 | 143 | 113 | 167 |
A Confidence interval (CI) is an interval of good estimates of the
unknown true population parameter. About a 95% confidence interval
for the mean, we can state that if we would repeat our sampling process
infinitely, 95% of the constructed confidence intervals would contain
the true population mean. In other words, there is a 95% chance of
selecting a sample such that the 95% confidence interval calculated from
that sample contains the true population mean.
Interpretation of the 95% confidence interval in our example:
-The values contained in the interval [138g/L to 143g/L] are good
estimates of the unknown mean whole blood hemoglobin concentration
in the population. In general, if we would repeat our sampling process
infinitely, 95% of such constructed confidence intervals would contain
the true mean hemoglobin concentration.
A Prediction interval (PI) is an estimate of an interval in which
a future observation will fall, with a certain confidence level,
given the observations that were already observed. About a 95%
prediction interval we can state that if we would repeat our sampling
process infinitely, 95% of the constructed prediction intervals would
contain the new observation.
Interpretation of the 95% prediction interval in the above example:
-Given the observed whole blood hemogblobin concentrations, the whole
blood hemogblobin concentration of a new sample will be between
113g/L and 167g/L with a confidence of 95%. In general, if we would
repeat our sampling process infinitely, 95% of the such constructed
prediction intervals would contain the new hemoglobin concentration
measurement.
Remark: Very often we will read the interpretation “The whole blood
hemogblobin concentration of a new sample will be between 113g/L and
167g/L with a probability of 95%.” (for example on
wikipedia).
This interpretation is correct in the theoretical situation where the
parameters (true mean and standard deviation) are known.
Estimating a prediction interval in R
First, let’s simulate some data. The sample size in the plot above was
(n=100). Now, to see the effect of the sample size on the width of the
confidence interval and the prediction interval, let’s take a “sample”
of 400 hemoglobin measurements using the same parameters:
set.seed(123)
hemoglobin<-rnorm(400, mean = 139, sd = 14.75)
df<-data.frame(hemoglobin)Although we don’t need a linear regression yet, I’d like to use the lm()
function, which makes it very easy to construct a confidence interval
(CI) and a prediction interval (PI). We can estimate the mean by fitting
a “regression model” with an intercept only (no slope). The default
confidence level is 95%.
-Confidence interval:
CI<-predict(lm(df$hemoglobin~ 1), interval="confidence")
CI[1,]## fit lwr upr
## 139.2474 137.8425 140.6524The CI object has a length of 400. But since there is no slope in our
“model”, each row is exactly the same.
-Prediction interval:
PI<-predict(lm(df$hemoglobin~ 1), interval="predict") ## Warning in predict.lm(lm(df$hemoglobin ~ 1), interval = "predict"): predictions on current data refer to _future_ responsesPI[1,]## fit lwr upr
## 139.2474 111.1134 167.3815We get a “warning” that “predictions on current data refer to future
responses”. That’s exactly what we want, so no worries there. As you
see, the column names of the objects CI and PI are the same.
Now, let’s visualize the confidence and the prediction interval.
The code below is not very elegant but I like the result (tips are
welcome :-))
library(ggplot2)
limits_CI <- aes(x=1.3 , ymin=CI[1,2], ymax =CI[1,3])
limits_PI <- aes(x=0.7 , ymin=PI[1,2], ymax =PI[1,3])
PI_CI<-ggplot(df, aes(x=1, y=hemoglobin)) +
geom_jitter(width=0.1, pch=21, fill="grey", alpha=0.5) +
geom_errorbar (limits_PI, width=0.1, col="#1A425C") +
geom_point (aes(x=0.7, y=PI[1,1]), col="#1A425C", size=2) +
geom_errorbar (limits_CI, width=0.1, col="#8AB63F") +
geom_point (aes(x=1.3, y=CI[1,1]), col="#8AB63F", size=2) +
scale_x_continuous(limits=c(0,2))+
scale_y_continuous(limits=c(95,190))+
theme_bw()+ylab("Hemoglobin concentration (g/L)") +
xlab(NULL)+
geom_text(aes(x=0.6, y=160, label="Predictionninterval",
hjust="right", cex=2), col="#1A425C")+
geom_text(aes(x=1.4, y=140, label="Confidenceninterval",
hjust="left", cex=2), col="#8AB63F")+
theme(legend.position="none",
axis.text.x = element_blank(),
axis.ticks.x = element_blank())
PI_CI
The width of the confidence is very small, now that we have this large
sample size (n=400). This is not surprising, as the estimated mean is
the only source of uncertainty. In contrast, the width of the prediction
interval is still substantial. The prediction interval has two sources
of uncertainty: the estimated mean (just like the confidence interval)
and the random variance of new observations.
Example: comparing a new with a reference measurement method.
A prediction interval can be useful in the case where a new method
should replace a standard (or reference) method. If we can predict well
enough what the measurement by the reference method would be, (given the
new method), than the two methods give similar information and the new
method can be used.
For example in (Tian, 2017) a new spectral method (Near-Infra-Red) to
measure hemoglobin is compared with a Golden Standard. In contrast with
the Golden Standard method, the new spectral method does not require
reagents. Moreover, the new method is faster. We will investigate
whether we can predict well enough, based on the measured concentration
of the new method, what the measurement by the Golden Standard would be.
(note: the measured concentrations presented below are fictive)
Hb<- read.table("https://usercontent.one/wp/rforbiostatistics.colmanstatistics.be/wp-content/uploads/2023/03/Hb.txt",
header = TRUE)
library(pander)
pander(head(Hb))| New | Reference |
|---|---|
| 84.97 | 87.24 |
| 99.91 | 103.4 |
| 111.8 | 116.7 |
| 117 | 116.7 |
| 118.1 | 113.5 |
| 118.2 | 121.7 |
plot(Hb$New, Hb$Reference,
xlab="Hemoglobin concentration (g/L) - new method",
ylab="Hemoglobin concentration (g/L) - reference method")
Prediction Interval based on linear regression:
Now, let’s fit a linear regression model predicting the hemogoblin
concentrations measured by the reference method, based on the
concentrations measured with the new method.
fit.lm <- lm(Hb$Reference ~ Hb$New)
plot(Hb$New, Hb$Reference,
xlab="Hemoglobin concentration (g/L) - new method",
ylab="Hemoglobin concentration (g/L) - reference method")
cat ("Adding the regression line:")Adding the regression line:
abline (a=fit.lm$coefficients[1], b=fit.lm$coefficients[2] )
cat ("Adding the identity line:")Adding the identity line:
abline (a=0, b=1, lty=2)
If both measurement methods would exactly correspond, the intercept
would be zero and the slope would be one (=“identity line”, dotted
line).
Now let’s calculate the confidence interval for this linear regression.
CI_ex <- predict(fit.lm, interval="confidence")
colnames(CI_ex)<- c("fit_CI", "lwr_CI", "upr_CI")And the prediction interval:
PI_ex <- predict(fit.lm, interval="prediction")## Warning in predict.lm(fit.lm, interval = "prediction"): predictions on current data refer to _future_ responsescolnames(PI_ex)<- c("fit_PI", "lwr_PI", "upr_PI")We can combine those results in one dataframe and plot both the
confidence interval and the prediction interval
Hb_results<-cbind(Hb, CI_ex, PI_ex)
pander(head(Hb_results))| New | Reference | fit_CI | lwr_CI | upr_CI | fit_PI | lwr_PI | upr_PI |
|---|---|---|---|---|---|---|---|
| 84.97 | 87.24 | 90.58 | 87.39 | 93.76 | 90.58 | 82.14 | 99.02 |
| 99.91 | 103.4 | 103.8 | 101.4 | 106.2 | 103.8 | 95.66 | 112 |
| 111.8 | 116.7 | 114.4 | 112.6 | 116.2 | 114.4 | 106.4 | 122.4 |
| 117 | 116.7 | 119 | 117.4 | 120.5 | 119 | 111 | 126.9 |
| 118.1 | 113.5 | 120 | 118.5 | 121.5 | 120 | 112 | 127.9 |
| 118.2 | 121.7 | 120.1 | 118.6 | 121.6 | 120.1 | 112.1 | 128 |
Visualizing the CI (in green) and the PI (in blue):
plot(Hb$New, Hb$Reference,
xlab="Hemoglobin concentration (g/L) - new method",
ylab="Hemoglobin concentration (g/L) - reference method")
Hb_results_s <- Hb_results[order(Hb_results$New),]
lines (x=Hb_results_s$New, y=Hb_results_s$fit_CI)
lines (x=Hb_results_s$New, y=Hb_results_s$lwr_CI,
col="#8AB63F", lwd=1.2)
lines (x=Hb_results_s$New, y=Hb_results_s$upr_CI,
col="#8AB63F", lwd=1.2)
lines (x=Hb_results_s$New, y=Hb_results_s$lwr_PI,
col="#1A425C", lwd=1.2)
lines (x=Hb_results_s$New, y=Hb_results_s$upr_PI,
col="#1A425C", lwd=1.2)
abline (a=0, b=1, lty=2)
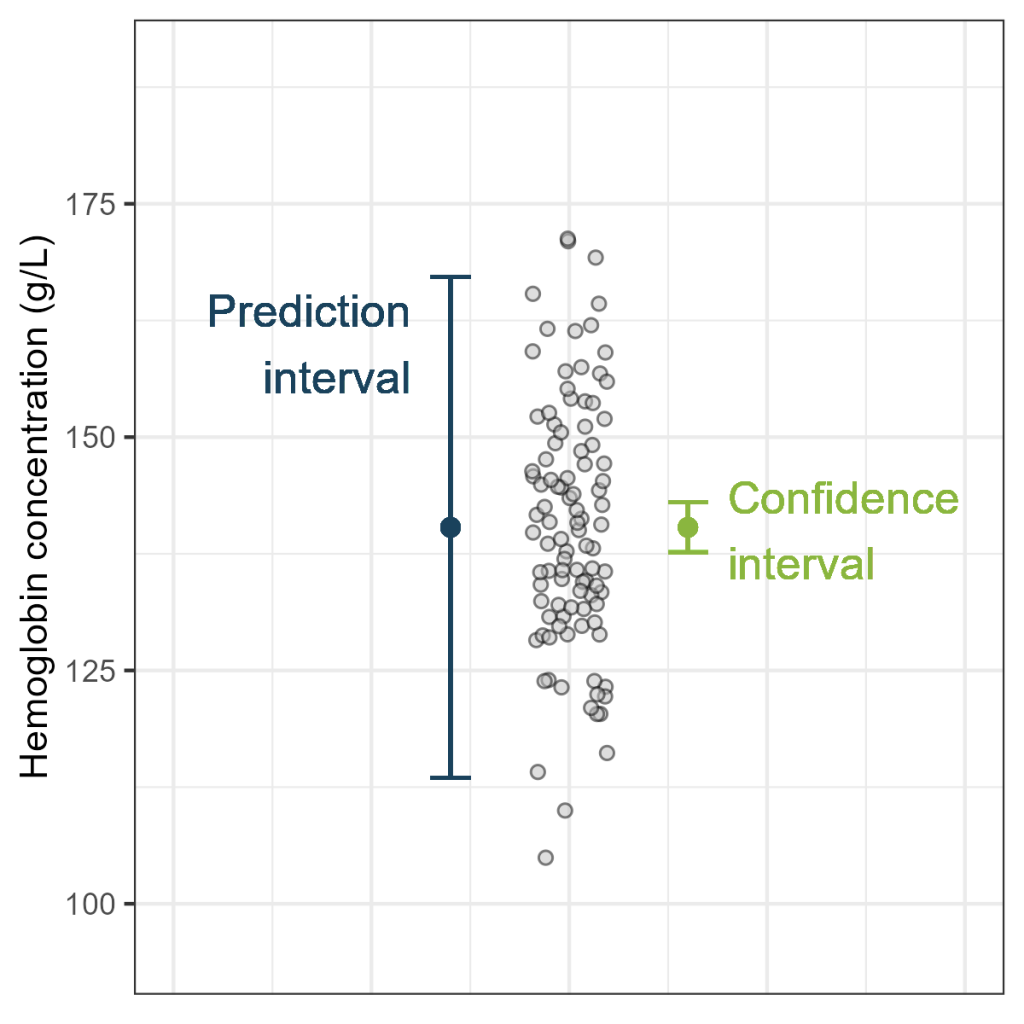
In (Bland, Altman 2003) it is proposed to calculate the average width of
this prediction interval, and see whether this is acceptable. Another
approach is to compare the calculated PI with an “acceptance interval”.
If the PI is inside the acceptance interval for the measurement range of
interest (see Francq, 2016).
In the above example, both methods do have the same measurement scale
(g/L), but the linear regression with prediction interval is
particularly useful when the two methods of measurement have different
units.
However, the method has some disadvantages:
- Predictions intervals are very sensitive to deviations from the
normal distribution. - In “standard” linear regression (or Ordinary Least Squares (OLS)
regression),the presence of measurement error is allowed for the
Y-variable (here, the reference method) but not for the X-variable
(the new method). The absence of errors on the x-axis is one of the
assumptions. Since we can expect some measurement error for the new
method, this assumption is violated here.
Taking into account errors on both axes
In contrast to Ordinary Least Square (OLS) regression, Bivariate Least
Square (BLS) regression takes into account the measurement errors of
both methods (the New method and the Reference method). Interestingly,
prediction intervals calculated with BLS are not affected when the axes
are switched (del Rio, 2001).
In 2017, a new R-package BivRegBLS was released. It offers several
methods to assess the agreement in method comparison studies, including
Bivariate Least Square (BLS) regression.
If the data are unreplicated but the variance of the measurement error
of the methods is known, The BLS() and XY.plot() functions can be used
to fit a bivariate Least Square regression line and corresponding
confidence and prediction intervals.
library (BivRegBLS)
Hb.BLS = BLS (data = Hb, xcol = c("New"),
ycol = c("Reference"), var.y=10, var.x=8, conf.level=0.95)
XY.plot (Hb.BLS,
yname = "Hemoglobin concentration (g/L) - reference method",
xname = "Hemoglobin concentration (g/L) - new method",
graph.int = c("CI","PI"))
Now we would like to decide whether the new method can replace the
reference method. We allow the methods to differ up to a given
threshold, which is not clinically relevant. Based on this threshold an
“acceptance interval” is created. Suppose that differences up to 10 g/L
(=threshold) are not clinically relevant, then the acceptance interval
can be defined as Y=X???, with ?? equal to 10. If the PI is inside the
acceptance interval for the measurement range of interest then the two
measurement methods can be considered to be interchangeable (see Francq,
2016).
The accept.int argument of the XY.plot() function allows for a
visualization of this acceptance interval
XY.plot (Hb.BLS,
yname = "Hemoglobin concentration (g/L) - reference method",
xname = "Hemoglobin concentration (g/L) - new method",
graph.int = c("CI","PI"),
accept.int=10)
For the measurement region 120g/L to 150 g/L, we can conclude that the
difference between both methods is acceptable. If the measurement
regions below 120g/l and above 150g/L are important, the new method
cannot replace the reference method.
Regression on replicated data
In method comparison studies, it is advised to create replicates (2 or
more measurements of the same sample with the same method). An example
of such a dataset:
Hb_rep <- read.table("https://usercontent.one/wp/rforbiostatistics.colmanstatistics.be/wp-content/uploads/2023/03/Hb_rep.txt",
header = TRUE)
pander(head(Hb_rep ))| New_rep1 | New_rep2 | Ref_rep1 | Ref_rep2 |
|---|---|---|---|
| 88.25 | 94.98 | 90.17 | 84.01 |
| 109.1 | 109.2 | 106.9 | 98.17 |
| 114.6 | 122.5 | 116.2 | 118.2 |
| 120.2 | 114.6 | 114.5 | 104.3 |
| 108.4 | 110.7 | 116.5 | 108.7 |
| 125.9 | 124.4 | 112.6 | 112.4 |
When replicates are available, the variance of the measurement errors
are calculated for both the new and the reference method, and used to
estimate the prediction interval. Again, the BLS() function and the
XY.plot() function are used to estimate and plot the BLS regression
line, the corresponding CI and PI.
Hb_rep.BLS = BLS (data = Hb_rep,
xcol = c("New_rep1", "New_rep2"),
ycol = c("Ref_rep1", "Ref_rep2"),
qx = 1, qy = 1,
conf.level=0.95, pred.level=0.95)
XY.plot (Hb_rep.BLS,
yname = "Hemoglobin concentration (g/L) - reference method",
xname = "Hemoglobin concentration (g/L) - new method",
graph.int = c("CI","PI"),
accept.int=10)
It is clear that the prediction interval is not inside the acceptance
interval here. The new method cannot replace the reference method. A
possible solution is to average the repeats. The BivRegBLS package can
create prediction intervals for the mean of (2 or more) future values,
too!
In the plot above, averages of the two replicates are calculated and
plotted. I’d like to see the individual measurements:
plot(x=c(Hb_rep$New_rep1, Hb_rep$New_rep2),
y=c(Hb_rep$Ref_rep1, Hb_rep$Ref_rep2),
xlab="Hemoglobin concentration (g/L) - new method",
ylab="Hemoglobin concentration (g/L) - reference method")
lines (x=as.numeric(Hb_rep.BLS$Pred.BLS[,1]),
y=as.numeric(Hb_rep.BLS$Pred.BLS[,2]),
lwd=2)
lines (x=as.numeric(Hb_rep.BLS$Pred.BLS[,1]),
y=as.numeric(Hb_rep.BLS$Pred.BLS[,3]),
col="#8AB63F", lwd=2)
lines (x=as.numeric(Hb_rep.BLS$Pred.BLS[,1]),
y=as.numeric(Hb_rep.BLS$Pred.BLS[,4]),
col="#8AB63F", lwd=2)
lines (x=as.numeric(Hb_rep.BLS$Pred.BLS[,1]),
y=as.numeric(Hb_rep.BLS$Pred.BLS[,5]),
col="#1A425C", lwd=2)
lines (x=as.numeric(Hb_rep.BLS$Pred.BLS[,1]),
y=as.numeric(Hb_rep.BLS$Pred.BLS[,6]),
col="#1A425C", lwd=2)
abline (a=0, b=1, lty=2)
Remarks
- Although not appropriate in the context of method comparisonstudies, Pearson correlation is still frequently used. See Bland &
Altman (2003) for an explanation on why correlations are not
advised. - Methods presented in this blogpost are not applicable to time-series
References
- Confidence interval and prediction interval:
Applied Linear Statistical Models, 2005, Michael Kutner, Christopher
Nachtsheim, John Neter, William Li. Section 2.5
-Prediction interval for method comparison:
Bland, J. M. and Altman, D. G. (2003), Applying the right statistics:
analyses of measurement studies. Ultrasound Obstet Gynecol, 22: 85-93.
<doi:10.1002/uog.12> section: “Appropriate use of regression”.
Francq, B. G., and Govaerts, B. (2016) How to regress and predict in a
Bland-Altman plot? Review and contribution based on tolerance intervals
and correlated-errors-in-variables models. Statist. Med., 35: 2328-2358.
doi: 10.1002/sim.6872.
del Rio, F. J., Riu, J. and Rius, F. X. (2001), Prediction intervals in
linear regression taking into account errors on both axes. J.
Chemometrics, 15: 773-788. <doi:10.1002/cem.663>
-Example of a method comparison study:
H. Tian, M. Li, Y. Wang, D. Sheng, J. Liu, and L. Zhang, “Optical
wavelength selection for portable hemoglobin determination by
near-infrared spectroscopy method,” Infrared Phys. Techn 86, 98-102
(2017). doi.org/10.1016/j.infrared.2017.09.004.
-The predict() and lm() functions of R:
Chambers, J. M. and Hastie, T. J. (1992) Statistical Models in S.
Wadsworth & Brooks/Cole.